Algoritma
Dijkstra sesuai dengan penemunya Edsger Dijkstra, adalah
sebuah algoritma yang dipakai dalam memecahkan masalah jarak terpendek untuk
sebuah graf berarah.
Algoritma ini dipublikasikan pada tahun 1959 dalam jurnal Numerische
Mathematik yang berjudul “A Note on Two Problems in Connexion with Graphs”. Permasalahan
rute terpendek dari sebuah titik ke titik akhir lain adalah sebuah masalah
optimasi yang banyak digunakan untuk menguji sebuah algoritma yang diusulkan. Permasalahan rute terpendek dianggap cukup
baik untuk memperbaiki masalah optimasi, karena permasalahannya hanya
menjumlahkan seluruh edge atau sisi yang dilalui namun memiliki banyak pilihan
solusi.
Menurut Andrew
Goldberg, seorang peneliti Microsoft Research Silicon Valley, mengatakan terdapat
banyak alasan mengapa peneliti terus mempelajari masalah pencarian jalan
terpendek, karena jalan terpendek adalah masalah optimasi yang relevan untuk
berbagai macam aplikasi, seperti jaringan routing, game, desain sirkuit, dan
pemetaan. Diskripsi matematis untuk grafik dapat diwakili G = {V. E}, yang
berarti sebuah (Grafik = G) didefinisikan oleh satu set simpul (Vertex = V) dan
(Edge = E).
Contoh,
hitunglah jarak terdekat dari V1 ke V7 pada gambar berikut ini :
Hasil
setiap stepnya dapat dilihat pada tabel berikut ini :
Dengan
demikian jarak terpendek dari V1 ke V7 adalah 16 dengan jalur V1->V2->V3->V5->V6->V7
Flowchart
algoritma Djikstra :
Jadi,
algoritma Dijkstra ini bertujuan untuk menemukan jalur terpendek berdasarkan
bobot terkecil dari satu titik ke titik lainnya. Misalnya titik mengambarkan
gedung dan garis menggambarkan jalan, maka algoritma Dijkstra melakukan
kalkulasi terhadap semua kemungkinan bobot terkecil dari setiap titik.
Algoritma
Greedy adalah jenis algoritma yang
menggunakan pendekatan penyelesaian masalah dengan mencari nilai maksimum
sementara pada setiap langkahnya. Nilai maksimum sementara ini dikenal dengan
istilah local maximum. Kebanyakan kasus, algoritma Greedy tidak akan
menghasilkan solusi paling optimal, begitupun pada umumnya memberikan solusi
yang mendekati nilai optimum dalam waktu yang cukup cepat. Sebagai contoh dari
penyelesaian masalah dengan algoritma Greedy, mari kita lihat sebuah masalah
yang sering kita jumpai dalam kehidupan sehari-hari yaitu mencari jarak
terpendek dari peta. Misalkan kita ingin bergerak dari titik A ke titik B, dan
kita telah menemukan beberapa jalur dari peta :
Dari
peta yang ditampilkan di atas, dapat kita lihat bahwa terdapat beberapa jalur
dari titik A ke titik B. Sistem peta pada gambar secara otomatis telah memilih
jalur terpendek yakni berwarna biru. Kita akan mencoba mencari jalur terpendek
juga, dengan menggunakan algoritma Greedy.
Langkah
pertama yang harus kita lakukan adalah memilih struktur data yang tepat untuk
digunakan dalam merepresentasikan peta. Jika kita lihat kembali, sebuah peta
seperti pada gambar di atas pada dasarnya hanya menunjukkan titik-titik yang
saling berhubungan, dengan jarak tertentu pada masing-masing titik tersebut.
Misalnya, peta di atas dapat direpresentasikan dengan titik-titik penghubung
seperti berikut ini :
Dari
gambar di atas, kita dapat melihat bagaimana sebuah peta jalur perjalanan dapat
direpresentasikan dengan menggunakan graph, yang lebih spesifiknya adalah graph
berarah. Maka dari itu, untuk menyelesaikan permasalahan jarak terpendek ini kita
akan menggunakan struktur data graph untuk merepresentasikan peta. Berikut graph
yang akan digunakan :
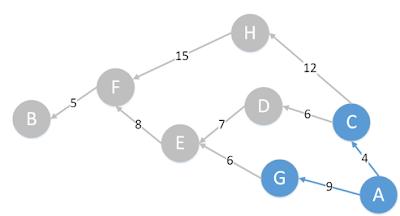
Untuk
mencari jarak terpendek dari A ke B, sebuah algoritma Greedy akan menjalankan
langkah-langkah seperti berikut :
1. Kunjungi satu titik pada graph, dan
ambil seluruh titik yang dapat dikunjungi dari titik sekarang.
2. Cari local maximum ke titik
selanjutnya.
3. Tandai graph sekarang sebagai graph
yang telah dikunjungi, dan pindah ke local maximum yang telah ditentukan.
4. Kembali ke langkah pertama sampai
titik tujuan didapatkan.
Jika
mengaplikasikan langkah-langkah di atas pada graph A ke B sebelumnya maka kita
akan mendapatkan pergerakan seperti berikut :
1. Mulai dari titik A. Ambil seluruh
titik yang dapat dikunjungi.
2. Local maximum adalah ke titik C,
karena jarak ke titik C adalah yang paling dekat.
3. Tandai titik A sebagai titik yang
telah dikunjungi, dan pindah ke titik C.
4. Ambil seluruh titik yang dapat
dikunjungi dari titik C.
5. Local maximum adaah ke D, dengan
jarak 6.
6. Tandai C sebagai titik yang telah
dikunjungi, dan pindah ke D.
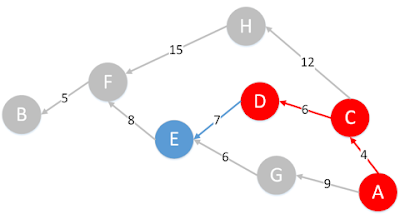
Dengan
menggunakan algoritma Greedy pada graph di atas, hasil akhir yang akan
didapatkan sebagai jarak terpendek adalah A-C-D-E-F-B. Hasi jarak terpendek
yang didapatkan ini tidak tepat dengan jarak terpendek yang sebenarnya adalah A-G-E-F-B.
Algoritma Greedy memang tidak selamanya memberikan solusi yang optimal,
dikarenakan pencarian local maximum pada setiap langkahnya, tanpa memperhatikan
solusi secara keseluruhan. Gambar berikut memperlihatkan bagaimana algoritma Greedy
dapat memberikan solusi yang kurang optimal :
Tetapi
ingat bahwa untuk kasus umum, kerap kali algoritma Greedy memberikan hasil yang
cukup baik dengan kompleksitas waktu yang cepat. Hal ini mengakibatkan
algoritma Greedy sering digunakan untuk menyelesaikan permasalahan kompleks
yang memerlukan kecepatan jawaban, bukan solusi optimal, misalnya pada game.
Dari
implementasi yang kita lakukan, dapat dilihat bagaimana algoritma Greedy
memiliki beberapa fungsionalitas dasar, yaitu :
1. Fungsi untuk melakukan penelusuran
masalah.
2. Fungsi untuk memilih local maximum
dari pilihan-pilihan pada tiap langkahnya.
3. Fungsi untuk mengisikan nilai local
maximum ke solusi keseluruhan.
4. Fungsi yang menentukan apakah solusi
telah didapatkan.
Algoritma
Greedy disusun oleh elemen-elemen yang digunakan dalam penerapan algoritma Greedy
antara lain :
1. Himpunan
kandidat, yaitu himpunan yang berisi elemen pembentuk solusi.
2. Himpunan
solusi, yaitu himpunan yang terpilih sebagai solusi persoalan.
3. Fungsi
seleksi, yaitu fungsi untuk memilih kandidat yang paling mungkin untuk mencapai
solusi optimal.
4. Fungsi
kelayakan, yaitu fungsi yang memeriksa apakah suatu kandidat yang dipilih dapat
memberikan solusi yang layak. Maksudnya yakni apakah kandidat tersebut bersama
dengan himpunan solusi yang sudah terbentuk tidak melanggar kendala yang ada.
5. Fungsi
solusi, yaitu fungsi untuk mengembalikan nilai boolean (true) jika himpunan
solusi yang sudah tebentuk merupakan solusi yang lengkap dan (false) jika
himpunan solusi belum lengkap.
6.
Fungsi objektif, yaitu fungsi yang
mengoptimalkan solusi.
Contohnya,
pada masalah penukaran uang :
· Himpunan
kandidat : himpunan koin yang merepresentasikan nilai 1, 5, 10, 25, paling
sedikit mengandung satu koin untuk setiap nilai.
· Himpunan
solusi : total nilai koin yang dipilih tepat sama jumlahnya dengan nilai uang
yang ditukarkan.
·
Fungsi
seleksi : pilihlah koin yang bernilai tertinggi dari himpunan kandidat yang
tersisa.
· Fungsi
layak : memeriksa apakah nilai total dari himpunan koin yang dipilih tidak
melebihi jumlah uang yang harus dibayar.
·
Fungsi
objektif : jumlah koin yang digunakan minimum.
Dalam
mencari sebuah solusi algoritma Greedy hanya memakai 2 buah macam persoalan optimasi,
yaitu :
·
Maksimasi (maxizimation).
·
Minimasi (minimization).
Jadi,
algoritma Greedy merupakan algoritma yang besifat heuristik, mencari nilai
maksimal sementara dengan harapan akan mendapatkan solusi yang cukup baik.
Meskipun tidak selalu mendapatkan solusi terbaik (optimum), algoritma Greedy umumnya
memiliki kompleksitas waktu yang cukup baik, sehingga algoritma ini sering
digunakan untuk kasus yang memerlukan solusi cepat meskipun tidak optimal
seperti sistem real-time atau game.
Dari
kedua algoritma ini, dapat saya simpulkan bahwa perbedaan dari kedua algoritma
tersebut terdapat pada masalah optimasi dalam sebuah program. Memang algoritma
Greedy memiliki keunggulan dibandingkan dengan algoritma Dijkstra yakni dalam
hal menyelesaikan permasalahan kompleks yang memerlukan kecepatan jawaban, bukan
solusi optimal. Maka dari itu, algoritma Dijkstra lah yang tepat untuk
memperbaiki masalah optimasi. Selain itu, kedua algoritma memiliki kesamaan
dalam hal menentukan jarak terpendek
Sumber referensi :